Atomic and Nuclear Physics (Core)
Syllabus:
7.1 - The atom
7.1 - The atom
7.1.2 - Outline the evidence that supports a nuclear model of the atom
7.1.3 - Outline one limitation of the simple model of the nuclear atom
7.1.4 - Outline evidence for the existence of atomic energy levels
7.1.5 - Explain the term nuclide, isotope and nucleon
7.1.6 - Define nucleon number A, proton number Z and neutron number N
7.1.7 - Describe the interactions in a nucleus
7.2 - Radioactive Decay
7.2.1 - Describe the phenomenon of natural radioactive decay
7.2.2 - Describe the properties of alpha and beta particles and gamma radiation
7.2.3 - Describe the ionising properties of alpha and beta particles and gamma radiation
7.2.4 - Outline the biological effects of ionising radiation
7.2.5 - Explain why some nuclei are stable, while others are unstable.
7.2.6 - State that radioactive decay is a random and spontaneous process and that the rate of decay decreases exponentially with time.
7.2.7 - Define the term radioactive half-life.
7.2.8 - Determine the half-life of a nuclide from a decay curve.
7.2.9 - Solve radioactive decay problems involving integral numbers of half lives.
7.3 - Nuclear Reactions, fission and fusion
7.3.1 - Describe and give an example of an artificial (induced) transmutation
7.3.2 - Construct and complete nuclear equations
7.3.3 - Define the term unified atomic mass unit
7.3.4 - Apply the Einstein mass-energy equivalence relationship
7.3.5 - Define the concepts of mass defect, binding energy and binding energy per nucleon
7.3.6 - Draw and annotate a graph showing the variation with nucleon number of the binding energy per nucleon.
7.3.7 - Solve problems involving mass defect and binding energy
7.3.8 - Describe the processes of nuclear fission and nuclear fusion
7.3.9 - Apply the graph in 7.3.6 to account for energy release in the processes of fission and fusion
7.3.10 - State that nuclear fusion is the main source of the sun's energy
7.3.11 - Solve problems involving fission and fusion reactions.
-------------------------------------------------------------------------------------------------------------
The Atom
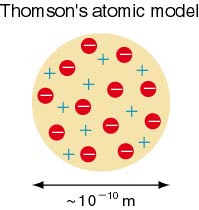
The plum pudding model of an atom was proposed in 1904. This model is composed of electrons surrounded by a soup of positive charge to balance the electrons.
http://www.kutl.kyushu-u.ac.jp
1. Rutherford's Explanation
2. Rutherford's Experiment
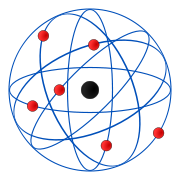
So, Rutherford suggested that atoms have a small dense nucleus and that electrons are in orbit around this nucleus. In 1909 the plum pudding model was tested by Ernest Rutherford, using the "gold foil" experiment. He reasoned that if Thomson was correct with the plum pudding model then the positive particles were spread out throughout the atom, so if he fired high velocity alpha particles at an atom there wouldn't be much to deflect the atoms. As he expected, most of the alpha particles went through the gold foil, however a few alpha particles rebounded directly backward.

http://www.iun.edu

http://www.iun.edu
Animations
2. Rutherford's Experiment
commons.wikimedia.org
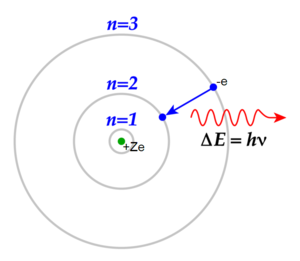
The Rutherford Model was soon replaced with the Bohr model which suggested that although electrons were in orbit around a nucleus, they were confined to atomic shells.
www.novaproj.org/.../300px-Bohr-atom-PAR.png
Simplified Explanation of the Bohr Model

www.novaproj.org/.../
Simplified Explanation of the Bohr Model
However, there are problems with the Bohr Model:
1. Simplified Model
2. The model is 2D not 3D
3. The nucleus stays together and doesn't repel protons (due to strong nuclear force)
4. Why aren't the electrons attracted to the nucleus
There are 2 pieces of evidence for Atomic Energy Levels:
- Emission Spectra
- Absorption Spectra
When a gaseous hydrogen atom in its ground state is excited by an input of energy, its electron is promoted from the lowest energy level to one of higher energy. The atom doesn't stay excited but emits the energy as electromagnetic radiation. This electron transition results in the release of a photon from the atom of an amount of energy equal to the difference in energy of the electronic energy levels involved in the transition. A prism can be used to separate the emitted electromagnetic radiation into its component frequencies. These are then put together to form an atomic emission spectrum. Each element has its own unique atomic emission spectra.

http://www.avogadro.co.uk/light/bohr/spectra.htm
Absorption Spectra:
If the difference between the lowest and highest energy level is E, then to make the transition between these two levels, an electron must absorb a photon of energy E. This creates a continuous spectrum crossed with dark lines. These lines correspond exactly to the lines in the emission spectrum of the same atom.

http://www.solarobserving.com/pics/hydrogen-spectra.jpg
Definitions:
Nuclide - A combination of protons and neutrons which form a nucleus
Isotope - Nuclei with the same number of protons but different number of neutrons
Nucleon - The name given to the particles of the nucleus (proton, neutron)
Nucleon Number - The number of neutrons plus protons in the nucleus (Top number)
Proton Number - The number of protons in the nucleus (bottom number)
Neutron Number - The number of neutrons in the nucleus
Ionizing Properties:
As alpha particles travel through the air they react with air molecules by taking 2 electrons from an air molecule and so becoming a neutral helium atom. This leaves the air molecule charged and the air is said to be ionized.
Beta particles and Gamma particles also cause ionization by removing electrons from the air molecules by collision with them, creating an electron-ion pair. This is used in particle detectors such as Geiger tubes and cloud and bubble chambers.
Effects of Radiation:
- Very High Dose
Nuclear Stability:
Radioactive half-life:
Radioactive half-life = the time it takes for the activity of a sample of the element to halve in value or the time it takes for half the atoms in a sample of elements to decay.
The more atoms in a sample, the more that are likely to decay at a given time.
The rate of decay of atoms at a given instant is proportional to the number of atoms of the element in the sample at that instant.
Theoretically it takes an infinite amount of time for the activity of the sample to fall to zero.
Nuclear Reactions, fission and fusion
In artificial transmutation, the nucleus is bombarded with high energy particles to induce transmutation.
Unified Atomic Mass Unit = 1/12 the mass of a nucleus of carbon-12
= 1.661 x 10-27 kg
Binding Energy:
Binding Energy can be looked at in terms of mass and energy.
In terms of mass, binding energy is the difference between the mass of the nucleus and the sum of the constituent (Different) parts.
In terms of energy, binding energy is the work required to pull apart the constituent parts of a nucleus.

Energy = mass x (speed of light)²
E = mc²
Mass Defect - Difference between rest mass and actual mass (together and apart)
Useful Numbers:
Mass of protons - 1.007825 kg
Mass of neutron - 1.008665 kg
Example:
Deuteron is made up of 1 proton and 1 neutron - Atomic mass = 2.014u
Mass difference = (1.007825+1.008665) - (2.014102) = 0.002388u
How much energy is needed to pull apart the constituents of the deuteron nucleus?
E = mc²
1 u = 931.5 MeV
0.002388u x 931.5Mev
= 2.224422MeV
Graph:
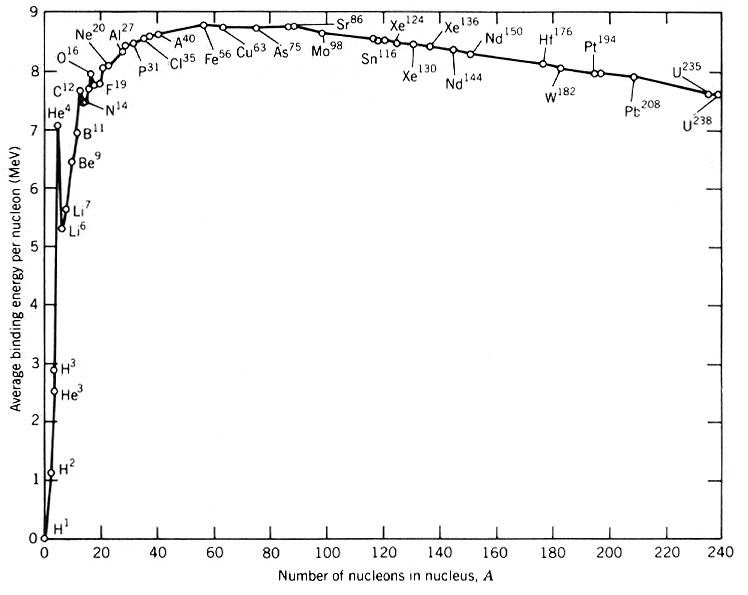
You should be able to draw the basic shape of the graph, know that:
In 1934, Fermi discovered that when uranium was bombarded with neutrons, radioactive products were produced. The energy released by the reaction appears in the form of kinetic energy of the fission nuclei and neutrons. The main problem with nuclear fission as a sustainable energy source is that the fission nuclei are often radioactive for a long time as they have long half lives. Isotopes, U-235 and U-238 can undergo nuclear fission.
Energy can also be obtained by fusing two nuclei together. To produce nuclear fusion, very high temperatures and pressures are needed, to overcome the coulomb repulsion force between them. The energy released appears in the form of kinetic energy of the helium nucleus and neutron. The advantage of fusion over fission is that there are no radioactive elements produced. However, it is difficult to obtain and maintain the high temperature and pressure needed for fusion.
In the sun's early life, due to gravitational collapse of the hydrogen making up the sun, the pressure and temperature became high enough to initiate fusion of the hydrogen. This fusion will continue until all the hydrogen is used up.
13.1 - Quantum Physics
13.1.1 - Describe the photoelectric effect
13.1.2 - Describe the concept of the photon, and use it to explain the photoelectric effect.
13.1.3 - Describe and explain an experiment to test the Einstein model.
13.1.4 -Solve problems involving the photoelectric effect.
13.1.5 - Describe the de Broglie hypothesis and the concept of matter waves.
13.1.6 - Outline an experiment to verify the de Broglie hypothesis.
13.1.7 - Solve problems involving matter waves
13.1.8 - Outline a laboratory procedure for producing and observing atomic spectra
13.1.9 - Explain how atomic spectra provide evidence for the quantization of energy in atoms.
13.1.10 - Calculate wavelengths of spectral lines from energy level differences and vice versa.
13.1.11 - Explain the origin of atomic energy levels in terms of the "electron in a box" model.
13.1.12 - Outline the Schrödinger model of the hydrogen atom.
13.1.13 - Outline the Heisenberg uncertainty principle with regard to position-momentum and time-energy
13.2 - Nuclear Physics
13.2.1 - Explain how the radii of nuclei may be estimated from charged particle scattering experiments.
13.2.2 - Describe how the masses of nuclei may be determined using a Bainbridge mass spectrometer.
13.2.3 - Describe one piece of evidence for the existence of nuclear energy levels.
13.2.4 - Describe Beta positive decay including the existence of the neutrino
13.2.5 - State the radioactive decay law as an exponential function and define the decay constant.
13.2.6 - Derive the relationship between decay constant and half life.
13.2.7 - Outline methods of measuring the half-life of an isotope.
13.2.8 - Solve problems involving radioactive half life.
-------------------------------------------------------------------------------------------------------------
Quantum Physics
The Photoelectric effect:
The photoelectric effect is the name given to the observation that when light is incident, electrons are emitted from the metal surface. These electrons which were emitted were called photoelectrons and could cause an electric current to flow. The photoelectric effect is caused by electrons on the surface of metal absorbing enough energy from incoming radiation to overcome the coulomb force of the protons in the nucleus. Whether photoelectrons were emitted or not depended on the frequency of the incident light.
For a given metal, there is a frequency below which no photoemission occurred, this is called the threshold frequency. By increasing the frequency of the incident radiation above this frequency, the kinetic energy of the photoelectrons increased.
"According to Einstein, when a photon collided with an electron in the surface of a metal it could either rebound or transfer all its energy to the electron. This explained why the number of electrons emitted was directly proportional to the intensity of the light, since intensity is a measure of the number of incident photons." - Source
For photoemission to occur, the energy of the incident photons needed to be enough to overcome the binding force of the nucleus. If there was extra incoming energy this could be converted to kinetic energy of the photoelectrons. The amount of energy needed to overcome the attractive force is called the work function.
If the energy of the photon is greater than the work function then we can apply the following equation
Einstein's photoelectric equation can therefore be written as:
hf = hf0 + eV
De Broglie:
The wave particle duality means that light has a dual nature, therefore it can behave as both a wave and a particle.
Louis de Broglie suggested that nature should be symmetrical and therefore if light had a particle nature, then particles should have a wave nature.
This wavelength of particles can be caled the de Broglie wavelength and the waves are called matter waves.
Sources:
Kerr G, Physics, 3rd Edition
Nuclide - A combination of protons and neutrons which form a nucleus
Isotope - Nuclei with the same number of protons but different number of neutrons
Nucleon - The name given to the particles of the nucleus (proton, neutron)
Nucleon Number - The number of neutrons plus protons in the nucleus (Top number)
Proton Number - The number of protons in the nucleus (bottom number)
Neutron Number - The number of neutrons in the nucleus
Radioactive Decay
Certain elements emit radiation without any external excitation, this is called radioactivity.
In 1896, Henri Becquerel found that Uranium salts which had been protected from excited radations for months still emitted penetrating radiation without any loss of intensity. He discovered that uranium itself was the cause of this radiation and that it was independent of pressure, temperature and chemical combination.
After Becquerel's discovery, Pierre and Maire Curie isolated 2 radioactive elements, polonium and radium, and in 1897, Rutherford found that 2 types of radiation occurred in radioactivity. He called the less penetrating rays Alpha and the more penetrating ones Beta.
In 1900, Paul Villiard, detected a 3rd type of radiation which was more penetrating than Beta. He called this type Gamma. Then in 1909, Rutherford identified that Alpha particles were helium nuclei.
All radiation comes from the nucleus.
Alpha Decay:
A nucleus of a radiative element which emits an alpha particle must transform into a nucleus of another element. This element has a nucleon number which changes by 4 and a proton number which changes by 2.
Beta Decay:
A free neutron decays into a proton and an electron. An antineutrino particle is also emitted in this decay. In order to conserve momentum and energy in Beta decay, the neutrino is needed. It has a zero rest mass and so travels at the speed of light and it is uncharged. In Beta decay in order to conserve other quantities, it must be an anti neutrino.
Certain elements emit radiation without any external excitation, this is called radioactivity.
In 1896, Henri Becquerel found that Uranium salts which had been protected from excited radations for months still emitted penetrating radiation without any loss of intensity. He discovered that uranium itself was the cause of this radiation and that it was independent of pressure, temperature and chemical combination.
After Becquerel's discovery, Pierre and Maire Curie isolated 2 radioactive elements, polonium and radium, and in 1897, Rutherford found that 2 types of radiation occurred in radioactivity. He called the less penetrating rays Alpha and the more penetrating ones Beta.
In 1900, Paul Villiard, detected a 3rd type of radiation which was more penetrating than Beta. He called this type Gamma. Then in 1909, Rutherford identified that Alpha particles were helium nuclei.
All radiation comes from the nucleus.
Alpha Decay:
A nucleus of a radiative element which emits an alpha particle must transform into a nucleus of another element. This element has a nucleon number which changes by 4 and a proton number which changes by 2.
Beta Decay:
A free neutron decays into a proton and an electron. An antineutrino particle is also emitted in this decay. In order to conserve momentum and energy in Beta decay, the neutrino is needed. It has a zero rest mass and so travels at the speed of light and it is uncharged. In Beta decay in order to conserve other quantities, it must be an anti neutrino.
As alpha particles travel through the air they react with air molecules by taking 2 electrons from an air molecule and so becoming a neutral helium atom. This leaves the air molecule charged and the air is said to be ionized.
Beta particles and Gamma particles also cause ionization by removing electrons from the air molecules by collision with them, creating an electron-ion pair. This is used in particle detectors such as Geiger tubes and cloud and bubble chambers.
Effects of Radiation:
- Very High Dose
- Damage to central nervous system
- Death in 2 or 3 days
- Damage to stomach and intestines
- Sickness, diarrhoea
- Death within weeks
- Loss of hair
- Bleeding
- Diarrhoea
- No such thing???
Nuclear Stability:
Radioactive half-life:
Radioactive half-life = the time it takes for the activity of a sample of the element to halve in value or the time it takes for half the atoms in a sample of elements to decay.
The more atoms in a sample, the more that are likely to decay at a given time.
The rate of decay of atoms at a given instant is proportional to the number of atoms of the element in the sample at that instant.
Theoretically it takes an infinite amount of time for the activity of the sample to fall to zero.
Nuclear Reactions, fission and fusion
In artificial transmutation, the nucleus is bombarded with high energy particles to induce transmutation.
Unified Atomic Mass Unit = 1/12 the mass of a nucleus of carbon-12
= 1.661 x 10-27 kg
Binding Energy:
Binding Energy can be looked at in terms of mass and energy.
In terms of mass, binding energy is the difference between the mass of the nucleus and the sum of the constituent (Different) parts.
In terms of energy, binding energy is the work required to pull apart the constituent parts of a nucleus.

Energy = mass x (speed of light)²
E = mc²
Mass Defect - Difference between rest mass and actual mass (together and apart)
Useful Numbers:
Mass of protons - 1.007825 kg
Mass of neutron - 1.008665 kg
Example:
Deuteron is made up of 1 proton and 1 neutron - Atomic mass = 2.014u
Mass difference = (1.007825+1.008665) - (2.014102) = 0.002388u
How much energy is needed to pull apart the constituents of the deuteron nucleus?
E = mc²
1 u = 931.5 MeV
0.002388u x 931.5Mev
= 2.224422MeV
Graph:

You should be able to draw the basic shape of the graph, know that:
- iron-56 is between 8 and 9
- Uranium-238 is between 7 and 8
- Hydrogen-1 is between 1 and 2
In 1934, Fermi discovered that when uranium was bombarded with neutrons, radioactive products were produced. The energy released by the reaction appears in the form of kinetic energy of the fission nuclei and neutrons. The main problem with nuclear fission as a sustainable energy source is that the fission nuclei are often radioactive for a long time as they have long half lives. Isotopes, U-235 and U-238 can undergo nuclear fission.
Energy can also be obtained by fusing two nuclei together. To produce nuclear fusion, very high temperatures and pressures are needed, to overcome the coulomb repulsion force between them. The energy released appears in the form of kinetic energy of the helium nucleus and neutron. The advantage of fusion over fission is that there are no radioactive elements produced. However, it is difficult to obtain and maintain the high temperature and pressure needed for fusion.
In the sun's early life, due to gravitational collapse of the hydrogen making up the sun, the pressure and temperature became high enough to initiate fusion of the hydrogen. This fusion will continue until all the hydrogen is used up.
Quantum and Nuclear Physics (HL)
Syllabus:13.1 - Quantum Physics
13.1.1 - Describe the photoelectric effect
13.1.2 - Describe the concept of the photon, and use it to explain the photoelectric effect.
13.1.3 - Describe and explain an experiment to test the Einstein model.
13.1.4 -Solve problems involving the photoelectric effect.
13.1.5 - Describe the de Broglie hypothesis and the concept of matter waves.
13.1.6 - Outline an experiment to verify the de Broglie hypothesis.
13.1.7 - Solve problems involving matter waves
13.1.8 - Outline a laboratory procedure for producing and observing atomic spectra
13.1.9 - Explain how atomic spectra provide evidence for the quantization of energy in atoms.
13.1.10 - Calculate wavelengths of spectral lines from energy level differences and vice versa.
13.1.11 - Explain the origin of atomic energy levels in terms of the "electron in a box" model.
13.1.12 - Outline the Schrödinger model of the hydrogen atom.
13.1.13 - Outline the Heisenberg uncertainty principle with regard to position-momentum and time-energy
13.2 - Nuclear Physics
13.2.1 - Explain how the radii of nuclei may be estimated from charged particle scattering experiments.
13.2.2 - Describe how the masses of nuclei may be determined using a Bainbridge mass spectrometer.
13.2.3 - Describe one piece of evidence for the existence of nuclear energy levels.
13.2.4 - Describe Beta positive decay including the existence of the neutrino
13.2.5 - State the radioactive decay law as an exponential function and define the decay constant.
13.2.6 - Derive the relationship between decay constant and half life.
13.2.7 - Outline methods of measuring the half-life of an isotope.
13.2.8 - Solve problems involving radioactive half life.
-------------------------------------------------------------------------------------------------------------
Quantum Physics
The Photoelectric effect:
The photoelectric effect is the name given to the observation that when light is incident, electrons are emitted from the metal surface. These electrons which were emitted were called photoelectrons and could cause an electric current to flow. The photoelectric effect is caused by electrons on the surface of metal absorbing enough energy from incoming radiation to overcome the coulomb force of the protons in the nucleus. Whether photoelectrons were emitted or not depended on the frequency of the incident light.
For a given metal, there is a frequency below which no photoemission occurred, this is called the threshold frequency. By increasing the frequency of the incident radiation above this frequency, the kinetic energy of the photoelectrons increased.
- Increasing the intensity of the incident light has no effect on the kinetic energy
- The number of electrons emitted is directly proportional to the intensity
- The emission started immediately the metal surface was irradiated
"According to Einstein, when a photon collided with an electron in the surface of a metal it could either rebound or transfer all its energy to the electron. This explained why the number of electrons emitted was directly proportional to the intensity of the light, since intensity is a measure of the number of incident photons." - Source
For photoemission to occur, the energy of the incident photons needed to be enough to overcome the binding force of the nucleus. If there was extra incoming energy this could be converted to kinetic energy of the photoelectrons. The amount of energy needed to overcome the attractive force is called the work function.
Energy = (Planck's constant) x (threshold frequency)
E = hf
Plank's Constant = 6.63 x 10^-34
E = hf
Plank's Constant = 6.63 x 10^-34
If the energy of the photon is greater than the work function then we can apply the following equation
(energy of incident photon) = (Energy required) + (Max KE)
hf = hf0 + E
Millikan then conducted an experiment to test the Einstein model. Electrons emitted by the photoelectric effect were collected and flowed through a meter to show a current. He then applied a positive voltage to the target metal until photoemission was stopped and the current dropped to zero. This potential is called the stopping potential. hf = hf0 + E
Einstein's photoelectric equation can therefore be written as:
hf = hf0 + eV
De Broglie:
The wave particle duality means that light has a dual nature, therefore it can behave as both a wave and a particle.
Louis de Broglie suggested that nature should be symmetrical and therefore if light had a particle nature, then particles should have a wave nature.
This wavelength of particles can be caled the de Broglie wavelength and the waves are called matter waves.
Momentum of the particle = (Planck's Constant)/ (de Broglie wavelength)
P = h/ wavelength
P = h/ wavelength
The de Broglie hypothesis can be confirmed experimentally using the Davisson-Germer experiment. They fired a beam of electrons, from an electron gun at a crystal of nickel (functioning as a diffraction grating). They observed that there was a maximum intensity at particular angles depending on the acceleration. The values they got for the de Broglie wavelength agreed with those predicted by de Broglie, proving his hypothesis correct.
Electron in a box model:
The electron in a box model assumes that the waves associated with the electron will be standing waves.
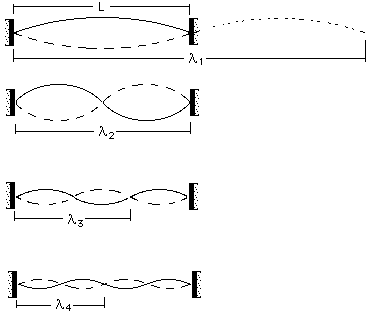
Electron in a box model:
The electron in a box model assumes that the waves associated with the electron will be standing waves.

Their wavelengths can be found as follows:
Wavelength = 2L
Wavelength = L
Wavelength = 2L/3
Wavelength = 2L/4
The Schrödinger Model:
In 1926, Schrödinger published his paper on wave mechanics. The Schrödinger model assumes electrons may be described by mathematical wave functions. In this model, the waves have undefined positions.
The Heisenberg Uncertainty Principle:
This uncertainty principle states that the simultaneous measurement of the position and momentum of a particle will always have some uncertainty. The more certain we are about the position of the particle the less certain we are about its momentum.
Nuclear Physics
Wavelength = 2L
Wavelength = L
Wavelength = 2L/3
Wavelength = 2L/4
The Schrödinger Model:
In 1926, Schrödinger published his paper on wave mechanics. The Schrödinger model assumes electrons may be described by mathematical wave functions. In this model, the waves have undefined positions.
The Heisenberg Uncertainty Principle:
This uncertainty principle states that the simultaneous measurement of the position and momentum of a particle will always have some uncertainty. The more certain we are about the position of the particle the less certain we are about its momentum.
Nuclear Physics
Sources:
Kerr G, Physics, 3rd Edition